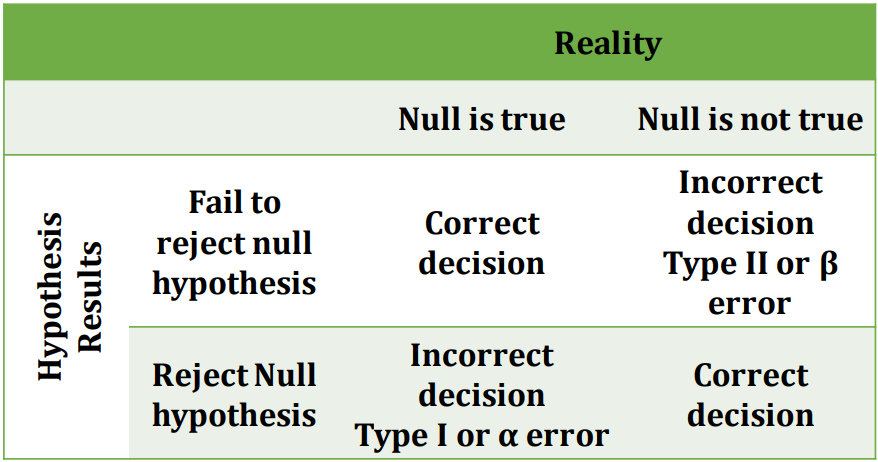
Evaluation Of Decision Error
-
Four possible outcomes that determine whether a
decision is correct or an error:
-
It is not possible to simultaneously commit a Type I(α)
error and Type II (β)decision error.
-
In short, either an alpha (α) or beta (β) decision error can
be made, but not both.
-
Probability of rejecting the null hypothesis when it is
true is called type I error, designated by Greek letter α
Alpha.
-
Example
- A toy manufacturing company set a limit of 2% defective from
the woodenparts it receives from its vendor.
- A sample of 500 parts out of 4000 lot size received revealed
that 11 parts were defective, translating to 2.2% greater than
2%.
- The customer rejectedthe Shipment.
- A 100% inspection from the vendor revealed that only 50 parts
were defective out of 4000 parts, i.e., 1.25% defective.
- In this case, only 1.25% of the parts were defective against an
acceptable level of 2% defective, and rejecting the shipment
was an error.
- In terms of hypothesis testing language, we say that we rejected
the Null Hypothesis, but the shipment wasnot substandard.
- We committed a Type 1 Error.
-
Probability of committing another type of error , called a
type II error, designated by Greek letter β ,beta
-
Type II error – Accepting the null hypothesis when it is
actually false
-
Example
- In the example, the toy manufacturer would commit a type II
error if a shipment from a supplier containing greater than 2%
defective, yetthe shipment was accepted.
- How could this happen?
- Suppose 9 out of the 500 parts in the sample tested were
substandard, leading to 1.8% defective. As per the guideline, the
sample contained less than 2% defective and hence was
accepted.
- What if, by chance, the 90 defective parts out of 4000 lots
leading to 2.25% defective greater than 2%
- Since the person doing analysis cannot study every item in the
population, thus there is the possibility of two types of errors,
Alpha error α, and beta errorβ