Distributions
-
Distributions are considered any population that has a
scattering of data. It's important to determine the kind
of distribution that the population has, so we can apply
the correct statistical methods when analyzing it.
- Distributions are classifiedas per the Data.
-
Continuous Distributions
- Normal Distribution
- Z Distribution
- Student’s T Distributions
- F distribution
- Chi-Square Distribution
-
Discrete Distributions
- Binomial distribution
- Poisson distribution
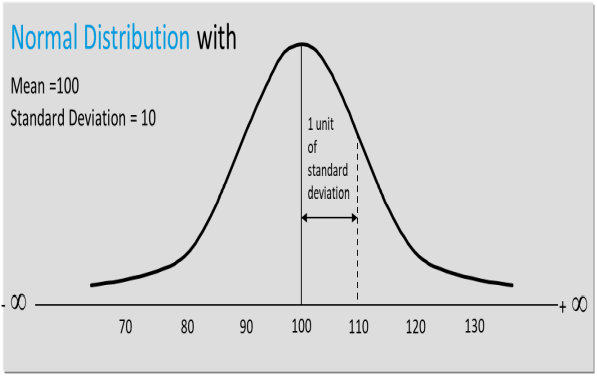
- Developed by astronomer Karl Gauss
- Most prominently used distribution in statistics
-
It comes close to fitting the actual frequency distribution of
many phenomena
-
Human characteristics such as weights, heights & IQ’s;
Physical process outputs such as yields
- It’s a Probability Distribution, illustrated as N,µ, σ
-
Higher frequency of values around the mean & lesser at
values away from mean
-
Continuous &
symmetrical
-
Total area under
the Normal curve
= 1
-
Mean = Median =
Mode
-
50% of Data lies
on either side of
the tolerance
-
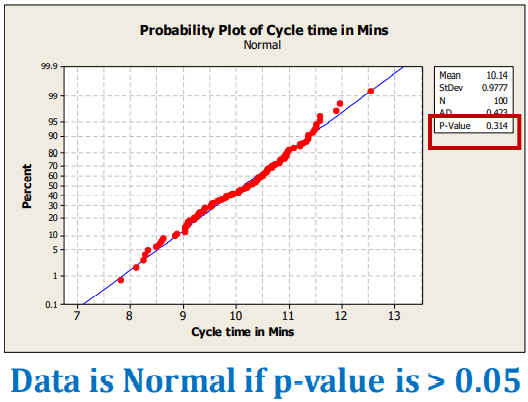
A Normality Test is used to check if the given data is
normally distributed or not.
-
It is important to check for normality because many
processes naturally follow the normal distribution,
especially in Manufacturing, but some do not, especially in
Service or Transactions
-
Many statistical tools assume data to be Normal while
performing various Tests
-
Lack of knowledge on
data distribution may
result in the wrong
Statistical tool's
usage, which might
result in incorrect
output and inference
of the data
-
The statistical
treatment of data is
different if the data is
non-normal
-
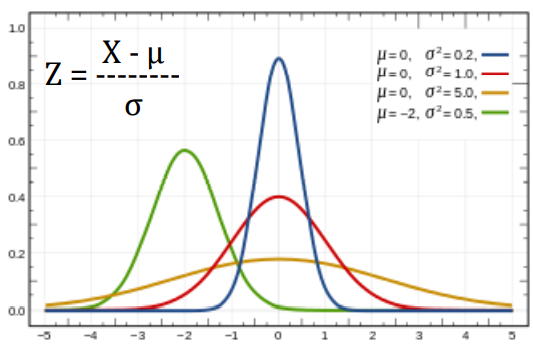
Z-distribution is a other way of naming
the Standard Normal distribution.
-
The Standard Normal Distribution is a specific instance of the
Normal Distribution that has a mean of ‘0’ and a Standard
Deviation of ‘1’ whereas there are no such limitations for
Normal distribution
-
The four curves shown
are Normal
distributions, but only
the red one is
Standard Normal since
its mean is zero, which
means that's where
it's centered, and its
standard deviation is
one.
-
Therefore, the Z value measures the distance between a
particular value of X and the mean in units of std dev.
-
By determining the z value, we can find the area or prob.
under the normal curve by referring to normal table.
-
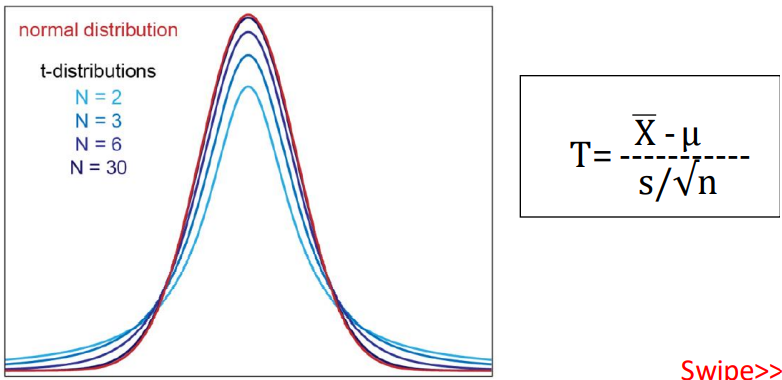
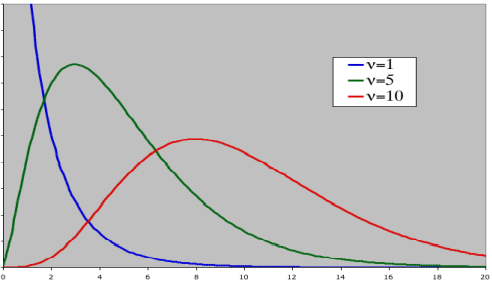
Student T distribution or T distribution is used for finding
confidence intervals for the population mean when the
sample size is less than 30, and the population standard
deviation is unknown.
-
If you need to evaluate something with a population greater
than 30, use the Z distribution
- T distribution is flatter and wider than the z distribution.
-
The T distribution becomes narrower (taller) as sample sizes
increase and gradually becomes very close to the normal
distribution. Both z and t distributions are symmetric and
bell-shaped, and both have a mean of zero.
-
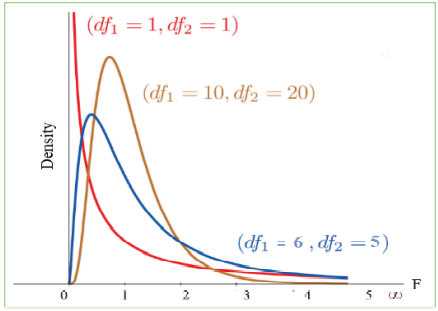
F-distribution is used to test for equality of variances from
two normal populations. The F-distribution is generally a
skewed distribution & also related to a chi-squared
distribution.
-
Characteristics of the F distribution
- The curve is positively skewed,and Its valueranges from 0 to ∞
- Skewness decreased with the increase of degrees of freedom of
numerator and denominator
- The value of F always positive or zero.No negative values
- If degrees of freedom increases, it will be more similar to the
symmetrical
-
Assumptions of the F distribution
- Assumes both populations are
normally distributed
- Both the populations are
independent of each other
- The larger sample variance
always goes in the numerator to
make the right-tailed test, and
the right-tailed tests are always
easy to calculate
-
The Chi-square distribution is a measure of the difference
between actual (observed) counts and expected counts.
-
It is most often for hypothesis tests (when there are >2
samples) and comparing proportions and in
determining confidence intervals (confidence interval for the
standard deviation).
-
Unlike the Normal distribution, the chi-square distribution is
not symmetric. Separate tables exist for the upper and lower
tails of the distribution.
-
This statistical test can be used to examine the hypothesis of
independence between two attribute variables and determine
if the attribute variables are related and fit a certain
probability distribution.
-
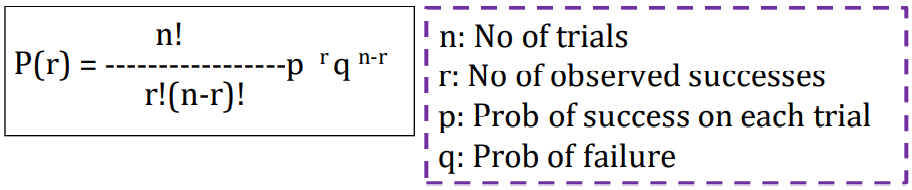
The binomial distribution is an example of discrete
distribution displaying data with only Two Possible
Outcomes, and each trial includes replacement. Information is
based on counts.
- Examples: Pass/ Fail, In/Out, Accept/Reject, Hot/Cold.
-
Binomial Distribution Assumptions:
- The Probability of success should be the same on every trial.
The Probability of success is constant.
- Two states.Twopossible outcomes.
- Independenttrials – trials are statistically independent.
- Use Binomial Distributionwhensamplingwith replacement.
-
To create a binomial distribution, we must know
- Number of trials
- Probability of success on each trial
-
The Poisson distribution is the discrete
probability distribution that shows how often an event is
likely to occur within a specified period of time. It is used for
independent events that occur at a constant rate within a
given interval of time.
-
For example, a service company receives an average number
of 100 service requests per day. If receiving any particular
piece of service request does not affect the arrival times of
future service requests, i.e., each service requests received are
independent of each other, then a reasonable assumption is
that the number of service requests received in a day obeys a
Poisson distribution.
-
Poisson Distribution Assumptions:
- An event can occur any number of times duringa time period.
- Events occur independently. Any event does not affect the
probability of another event occurring.
- The rate of occurrence is constant; that is, the rate does not
change based on time
Poisson Distribution formula is: P(X; λ) = (e
-λ ) (λX
) / X!
λ is the average number of events in the given time interval